Liquid crystals are found midway between liquids and solids in terms of their local symmetry and order. While they cannot be attributed a complete reference metric tensor as in solids, certain aspects of the local geometry must be maintained implying a reference geometry in some weaker sense. This gives rise to geometric frustration between local geometric constraints and the geometry of ambient space or topological constraints on defects in the liquid crystalline structure, which may lead to complex solutions and patterns. We study the topological rules of defects and defect interactions, as well as the equilibrium geometries, elasticity, dynamics, and stability of these topologically distinct states. These questions are essential in understanding phase transitions and bulk properties of materials, and may allow predicting and tuning material properties or designing exotic structures with unique topological attributes.
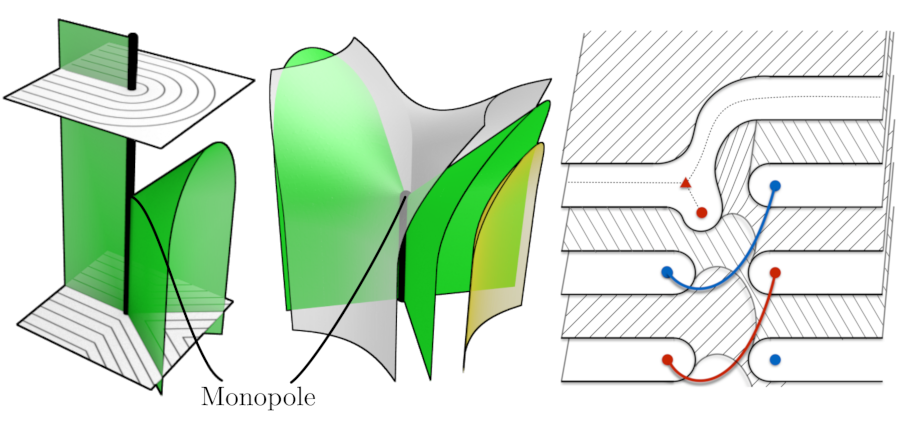
Smectic Point Defects on Line Defects (source)


