Classical cryptography relies on computational assumptions, such as the hardness of factoring, to deliver a wide range of functionalities. The advent of quantum information brought forward a completely different possibility: security based only on the fundamental laws of physics.
In the study of quantum cryptography we put quantum physics to work and utilise fundmental quantum phenomena to achieve powerful cryptographic tasks that cannot be achieved using classical means. Our main goal is proving the security of such protocols in a mathematically rigorous and experimentally relevant manner.
The most well-known example is that of quantum key distribution (QKD). In a QKD protocol two honest parties, called Alice and Bob, use entangled quantum states in order to create a shared private key, unknown to a quantum adversary, Eve, that can intercept the quantum communication between Alice and Bob or even manipulate the quantum devices that they use to execute the protocol. (See the figure below).
We study and prove the security of such protocols and others— we develop the mathematical techniques needed for, e.g., the analysis of the possible behaviours of quantum adversaries, and investigate the fundamental physics that underlies the possibility of achieving strong cryptographic statements. The work done in the group then acts as the theoretical groundwork for experiments implementing quantum cryptographic tasks.
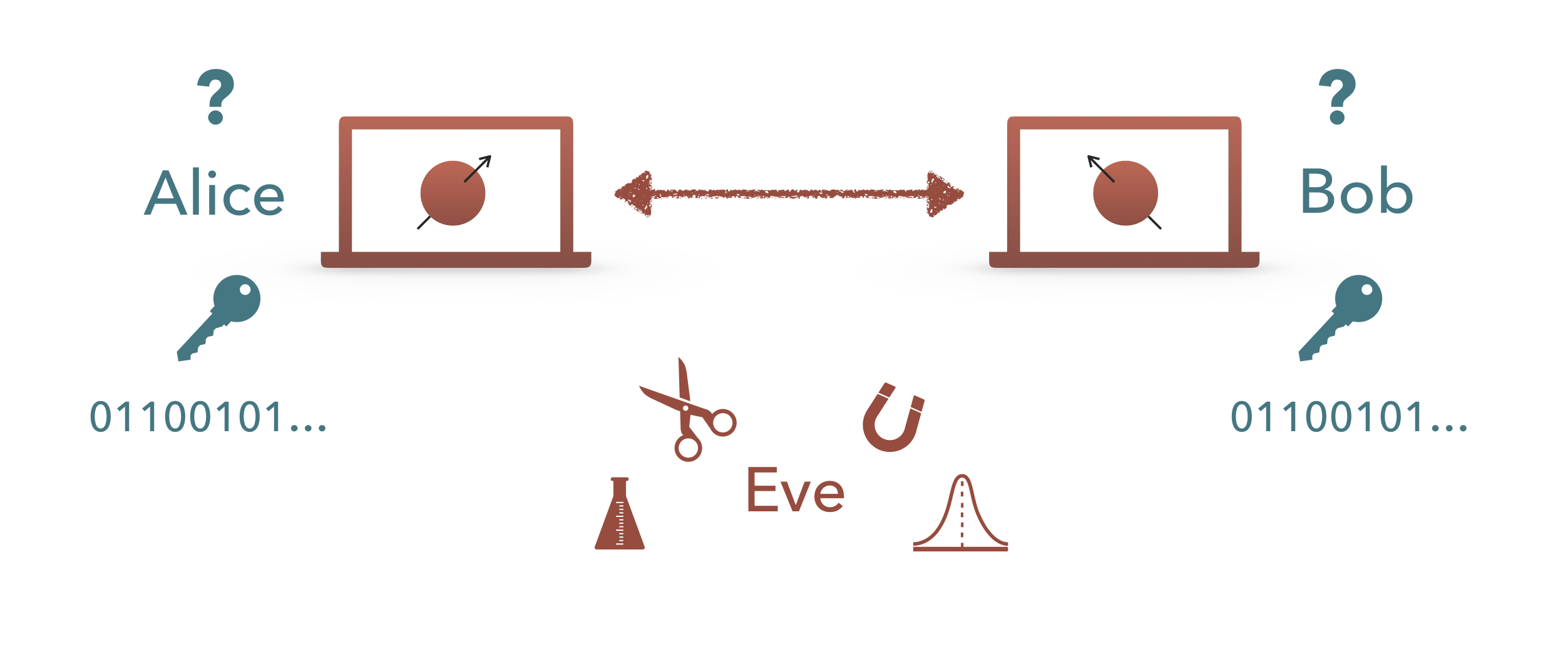
The basic setting of the task of quantum key distribution. Alice and Bob wish to create a shared key (sequence of bits) that is unknown to the quantum adversary Eve. Eve can manipulate and interact with the physical systems in various ways to gain information about the key. Our goal is to find a way for Alice and Bob to use their quantum devices such that Eve cannot gain significant information about the final key.


